The Illusion of The Illusion of The Illusion of Thinking

Это не просто кликбейтное название поста с мета-юмором, а реальное название препринта на arXiv, вышедшего 26 июня 2025 года. Очевидно, это была уже как минимум третья итерация какого-то спора – но в чём был спор и о чём вообще речь? Давайте разберёмся.

The Illusion of Thinking

История началась 7 июня, когда исследователи из Apple Shojaee et al. опубликовали статью с громким названием «Иллюзия мышления: понимание сильных и слабых сторон моделей рассуждения через призму сложности задач». Уже само название звучало очень громко, и результаты заявлялись интересные — неудивительно, что статья вызвала большой ажиотаж.

Методология исследования выглядела элегантно. Вместо стандартных математических тестов, которые могут быть «загрязнены» попаданием решений в обучающие выборки, учёные обратились к классическим головоломкам из информатики: ханойская башня, задачам о переправе через реку, Blocks World и т.д. Задумка была в том, чтобы плавно наращивать сложность, сохраняя логическую структуру. Например, в задаче о ханойской башне нужно было выписать последовательность ходов:

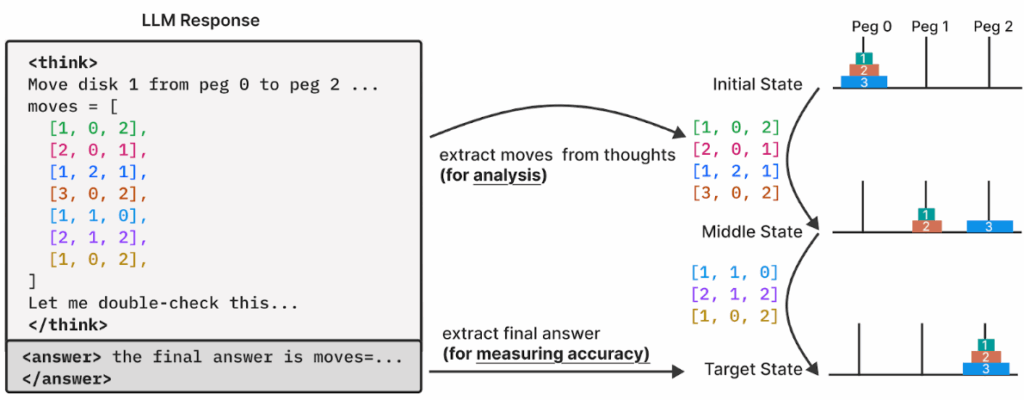
Результаты оказались обескураживающими. Исследователи выявили три режима работы моделей:

• при низкой сложности обычные модели неожиданно обходили рассуждающие модели;
• при средней сложности дополнительное время на обдумывание в продвинутых моделях давало некоторое преимущество; 
• но при высокой сложности все модели терпели полный крах.

Самое интересное (по мнению Shojaee et al.) — в том, что модели словно сдавались, не дойдя до предела. Вместо того чтобы попытаться что-то сделать со сложной задачей, модель заранее признавала поражение:

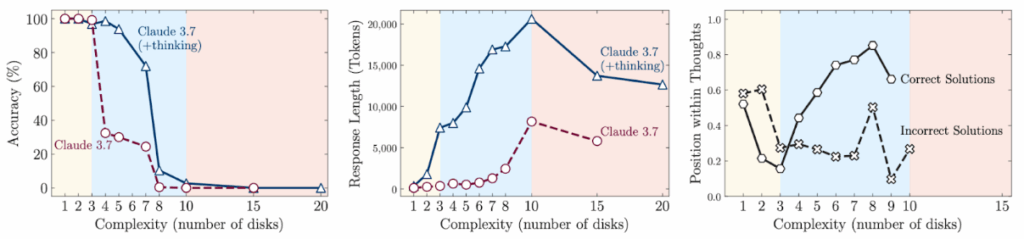
Более того, исследователи попробовали добавить в промпт буквально описание алгоритма, по которому решаются все эти задачи, и это моделям никак не помогло, результаты не изменились.

Что же, получается, не нужны рассуждающие модели? Не совсем…

The Illusion of the Illusion of Thinking

Реакция сообщества была предсказуемой: скептики торжествовали, энтузиасты искали изъяны в методологии Shojaee et al. И очень быстро нашли! Разных критических комментариев было много, но давайте разберём только самый знаменитый из них.

10 июня на arXiv появилась статья «The Illusion of the Illusion of Thinking» (Opus, Lawsen, June 10, 2025), первым автором которой значился… C. Opus из Anthropic. Та самая рассуждающая модель, которую только что обвинили в неспособности мыслить, выступила первым автором критического разбора этого обвинения. Вероятно, это нарушило какие-то правила arXiv, так что теперь авторство и название уже другие, но arXiv всегда помнит первую версию.

Автор-человек, Alex Lawsen из Open Philanthropy, позже признался, что всё началось как шутка. Из поста «When Your Joke Paper Goes Viral»: «Я подумал, что будет забавно написать ответную статью в соавторстве с Claude Opus. Изложил замеченные проблемы, дал их Claude, немного поработали вместе… собрал pdf да и поделился в Slack с друзьями».

Но шутки здесь оказалась только небольшая доля. Claude и Лоусен обнаружили в исследовании Apple три весьма критических изъяна.

Во-первых, модели там, где исследователи фиксировали «провал» в решении ханойских башен, чаще всего модели всего-навсего упирались в лимит токенов. Представьте, что вам дают решить задачу на умножение тысячезначных чисел и один небольшой листочек бумаги. Модели буквально писали в своих ответах: «Паттерн продолжается, но я остановлюсь, чтобы сэкономить токены» — а автоматическая система оценки засчитывала это как неудачу.

Вторая проблема была ещё более, гм, конфузной: задачи о переправе через реку для N ≥ 6 были математически неразрешимы из-за недостаточной вместимости лодки! Как выразились Claude и Лоусен, это «всё равно что штрафовать SAT-солвер за ответ “unsat” на неразрешимой формуле».

Ну и в-третьих, разумеется, когда вместо перечисления всех ходов модели попросили написать алгоритм решения, все они справились блестяще. Модели прекрасно знают, как решать Ханойские башни — но их заставляли выписывать 32767 ходов (для N=15) вместо демонстрации понимания принципа, а на это их «блокнотика» уже не хватало. Разумеется, именно поэтому алгоритм им и не помогал: модели прекрасно знают алгоритм для решения ханойских башен и сами, им не нужна в этом помощь.

The Illusion в кубе: реакции на реакцию

Реакция AI-сообщества и на статью, и на опровержение, написанное вместе с Claude, была неоднозначной. Многие, включая меня, соглашаются с критическими комментариями. Некоторые решили занять сторону Shojaee et al. и критиковать критику. И действительно, текст Claude и Лоусена содержал некоторые довольно очевидные ошибки (см., например, здесь).

Но всякий раз, когда люди пытались защитить оригинальную статью, а не искать недостатки в Opus, Lawsen (2025), они терпели неудачу. Как яркий пример я выделю пост Гэри Маркуса, в котором перечислены несколько аргументов против опровержений… но на их реальное содержание не даётся никакого существенного ответа. Более того, настоящая критика там смешивается с очевидными «соломенными чучелами» вроде «главный автор статьи был стажером» — может, Маркус и нашёл такой твит на просторах сети X, но разбирать этот «аргумент» наравне с аргументом «от LLM требовалось решать нерешаемые задачи», мягко скажем, некорректно. Гэри Маркус пошёл и ещё дальше: он даже опубликовал статью для The Guardian под названием «When billion-dollar AIs break down over puzzles a child can do, it’s time to rethink the hype», что, конечно же, породило свою собственную мини-волну хайпа, но это уже другая история.

Но я обещал третью производную. 16 июня вышла работа «The Illusion of the Illusion of the Illusion of Thinking», на этот раз в соавторстве G. Pro и V. Dantas. Кажется, потихоньку рождается новая академическая традиция…

Этот, уже третичный, анализ утверждает, что, хотя Claude и Лоусен действительно нашли контраргументы, которые сводят на нет самые серьёзные утверждения исходной статьи, всё же интересно было бы подробнее изучить природу ограничений рассуждающих моделей. Модель знает алгоритм и легко может записать его в виде кода, но действительно не способна без ошибок записать 32767 ходов подряд, нужных для решения ханойской башни с 15 дисками, даже при неограниченном бюджете токенов. Это тоже может быть интересным выводом из исследования.

Заключение

Конечно, у работы Shojaee et al. (2025) есть неустранимые недостатки. Наши методы оценки должны быть корректными и соответствовать системам, которые мы пытаемся оценить. Разумеется, стоит проверить, действительно ли тестовые головоломки имеют решения, прежде чем заявлять, что AI-модели не могут их решить. Но указывает ли эта работа на какие-то реальные ограничения, которые говорят нам что-то новое о современных AI-системах? Есть ли здесь какие-то уроки, которые можно извлечь?

Здесь я, пожалуй, просто порекомендую пост Лоуренса Чана. Он помещает все это в контекст давних дискуссий об ограничениях систем ИИ и нейронных сетей в частности, от книги Минского и Пейперта, критикующей перцептроны, до аргументов из вычислительной сложности (Chiang et al., 2023), набора данных ARC-AGI и гораздо более простого аргумента в духе Shojaee et al. (2025) о том, что LLM не могут умножать 15-значные числа. 

А вот motte-and-bailey мем от Чена, который кратко объясняет, почему (интерпретация Гэри Маркуса) статьи Shojaee et al. (2025) неверна:

В общем, на выходе ничего потрясающего основы из этой статьи, конечно, не получилось. Рассуждающие модели всё так же работают, это даже не то чтобы хороший пример jagged frontier возможностей LLM, который действительно существует. Но мне кажется, что случай интересный: во-первых, он породил интересную дискуссию, а во-вторых, в этой дискуссии уже открытым текстом слышен голос языковых моделей. Кажется, и академический мир уже не будет прежним…

Сергей Николенко

P.S. Прокомментировать и обсудить пост можно в канале “Sineкура”: присоединяйтесь!