A Mixed Blessing I: Mixtures of Experts from Committee Machines to LLMs

The world’s most powerful AI models are mostly asleep, just like our brains. Giant trillion-parameter models activate only a tiny fraction of their parameters for any given input, using mixtures of experts (MoE) to route the activations. MoE models began as a clever trick to cheat the scaling laws; by now, they are rapidly turning into the organizing principle of frontier AI models. In this post, we will discuss MoEs in depth, starting from the committee machines of the late 1980s and ending with the latest MoE-based frontier LLMs. We will mostly discuss LLMs and the underlying principles of MoE architectures, leaving vision-based and multimodal mixtures of experts for the second part.

Introduction

In December 2024, a relatively unknown Chinese AI lab called DeepSeek released a new model. As they say in Silicon Valley, it was a good model, sir. Their DeepSeek-V3 (DeepSeek AI, 2024), built with an architecture that has 671 billion parameters in total but activates only a fraction on each input, matched or exceeded the performance of models costing orders of magnitude more to train. One of their secrets was an architectural pattern that traces its roots back to the 1980s but has only recently become the organizing principle of frontier AI: Mixtures of Experts (MoE).

If you have been following AI developments, you may have noticed a curious pattern. Headlines about frontier models trumpet ever-larger parameter counts: GPT-4’s rumored 1.8 trillion, Llama 4 Behemoth’s 2 trillion parameters. But these models are still quite responsive, and can be run efficiently enough to serve millions of users. What makes it possible is that frontier models are increasingly sparse. They are not monolithic neural networks where every parameter activates on every input. Instead, they are built on mixture of experts (MoE) architectures that include routing systems that dynamically assemble specialized components, activating perhaps only 10-20% of their total capacity for any given task.

This shift from dense to sparse architectures may represent more than just an engineering optimization. It may be a fundamental rethinking of how intelligence should be organized—after all, biological neural networks also work in a sparse way, not every neuron in your brain fires even for a complex reasoning task. By developing MoE models with sparse activation, we can afford models with trillions of parameters that run on reasonable hardware, achieve better performance per compute dollar, and potentially offer more interpretable and modular AI systems.

Yet the journey of MoEs has been anything but smooth. For decades, these ideas had been considered too complex and computationally intensive for practical use. It took many hardware advances and algorithmic innovations to resurrect them, but today, MoE architectures power most frontier large language models (LLMs). In this deep dive, we will trace this remarkable evolution of mixture of experts architectures from their origins in 1980s ensemble methods to their current status as the backbone of frontier AI.

Before we begin, let me recommend a few surveys that give a lot more references and background than I could here: Cai et al. (2024), Masoudnia, Ebrahimpour (2024), and Mu, Lin (2025). To give you an idea of the scale of these surveys, here is a general timeline of recent MoE models by Cai et al. (2024) that their survey broadly follows:

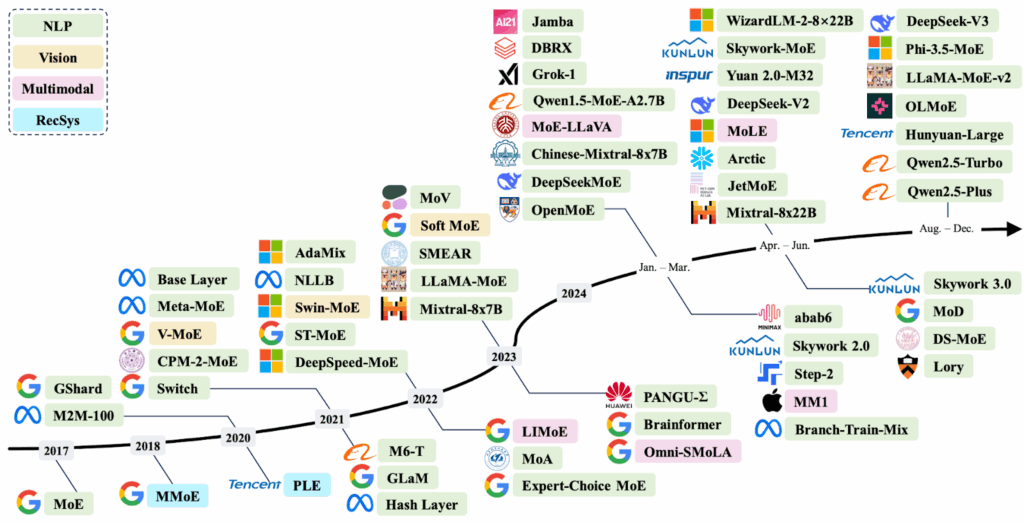
Naturally, I won’t be able to discuss all of this in detail, but I do plan two posts on the subject for you, and both will be quite long. 

In this first part, we discuss MoE architectures from their very beginnings in the 1980s to the latest LLMs, leaving the image processing and multimodal stuff for the second part. Here is my own timeline of the models and ideas and we touch upon in detail in this first part of the post; hopefully it will also serve as a plan for what follows:

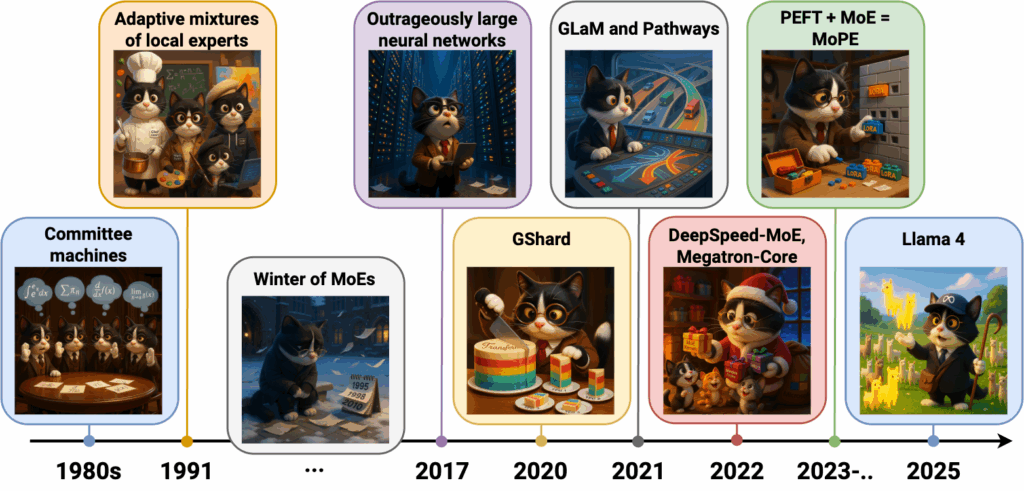
Let’s begin!

MoE Origins: From Ensemble Intuition to Hierarchical Experts

Despite their recent resurgence, mixtures of experts have surprisingly deep historical roots. To fully understand their impact and evolution, let us begin by tracing the origins of these ideas back to a much earlier and simpler era, long before GPUs and Transformer architectures started dominating AI research.

Committee Machines (1980s and 1990s)

The first appearance of models very similar to modern MoE approaches was, unsurprisingly, in ensemble methods, specifically in a class of models known as committee machines, emerging in the late 1980s and maturing through the early 1990s (Schwarze, Hertz, 1993; 1992).

These models combined multiple simple networks or algorithms—each independently rather weak—into a collectively strong predictor. Indeed, the boundary between committee machines and multilayered neural networks remained fuzzy; both combined multiple processing units, but committee machines emphasized the ensemble aspect while neural networks focused on hierarchical feature learning. For instance, here is an illustration by Schwarze and Hertz (1993) that looks just like a two-layered perceptron:

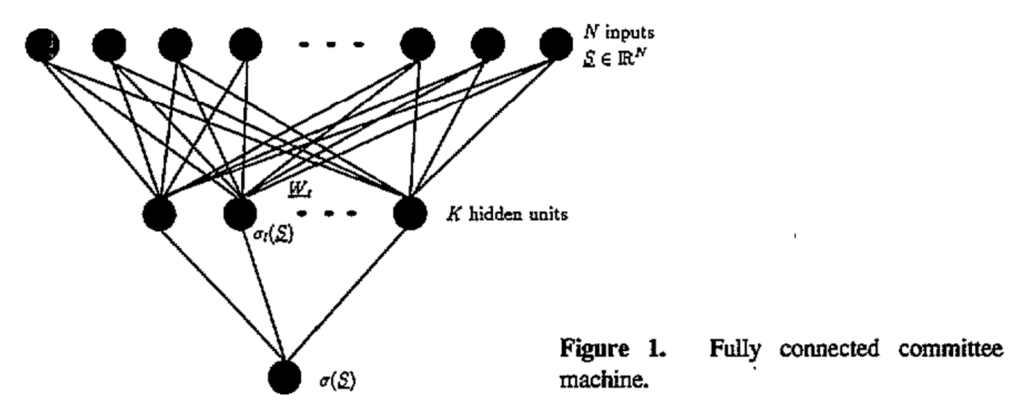
Early theoretical explorations into committee machines applied insights from statistical physics (Mato, Parga, 1992), analyzing how multiple hidden units, called “committee members”, could collaboratively provide robust predictions.

In their seminal 1993 work, Michael Perrone and Leon Cooper (the neurobiologist who was the C in BCM theory of learning in the visual cortex) demonstrated that a simple average of multiple neural network predictions could significantly outperform any single member. They found that ensembles inherently reduced variance and often generalized better, a cornerstone insight that I still teach every time I talk about ensemble models and committees in my machine learning courses.

But while averaging neural networks was powerful, it was also somewhat naive: all ensemble members contributed equally regardless of context or expertise. A natural next step was to refine ensembles by letting each member specialize, focusing their attention on different parts of the input space. This specialization led to the key innovation behind mixtures of experts: gating mechanisms.

First mixtures of experts (1991–1994)

The first “true” MoE model was introduced in a seminal 1991 paper titled “Adaptive Mixtures of Local Experts” and authored by a very impressive team of Robert Jacobs, Michael Jordan, Steven Nowlan, and Geoffrey Hinton. They transformed the general notion of an ensemble into a precise probabilistic model, explicitly introducing the gating concept. Their architecture had a “gating network”, itself a neural network, that learned to partition the input space and assign inputs probabilistically to multiple “expert” modules:

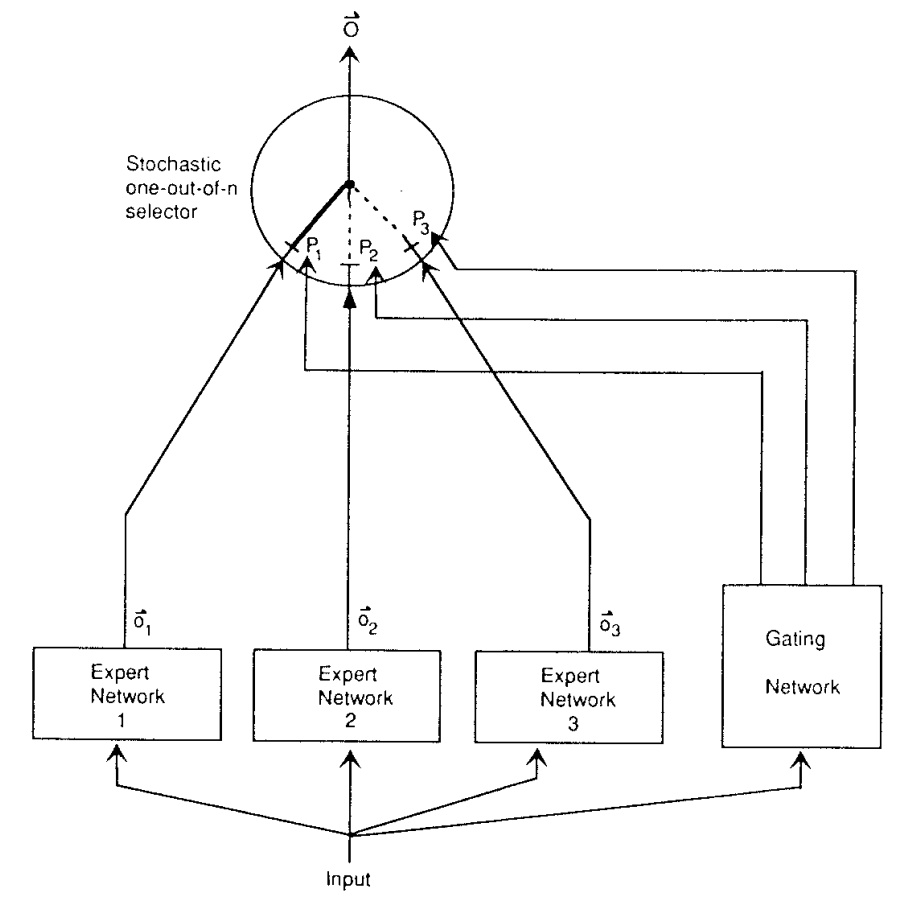
Each expert would handle a localized subproblem, trained jointly with the gating network via gradient descent, minimizing the squared prediction error. Note that in the 1990s, every expert would be activated on every input, sparse gating would come much later.

The follow-up work by Jordan and Jacobs extended this idea to hierarchical mixtures of experts (Jordan, Jacobs, 1991; 1993). Here, gating networks were structured into trees, where each node made a soft decision about passing data down one branch or another, progressively narrowing down to the most appropriate expert:

Importantly, Jacobs and Jordan also saw how to apply the expectation-maximization (EM) algorithm for maximum likelihood optimization of these networks, firmly establishing MoE as a principled statistical modeling tool. EM is a very important tool in every machine learning researcher’s toolbox, appearing wherever models contain a lot of hidden (latent) variables, and hierarchical MoEs are no exception.

In total, these seminal contributions introduced several fundamental concepts that are important for MoE architectures even today:

• softmax gating probabilities, today mirrored as router logits in Transformer-MoE layers;
• tree-structured gating networks, which are used in multi-layer or cascaded routing in modern implementations, and
• Expectation-Maximization training, which keeps inspiring auxiliary losses in contemporary MoE implementations to balance expert load and ensure specialization;

Moreover, back in the early 1990s the authors of these works also foresaw the benefits of modularity: experts could be independently updated, swapped, or fine-tuned; this is also widely used in today’s practice, as we will see below.

The “winter of MoEs” (mid-1990s to 2010s)

Given such promising beginnings, one might wonder why MoEs did not immediately revolutionize neural network research in the 1990s. Instead, mixtures of experts went through a period of dormancy lasting nearly two decades; they would resurface only in 2017.

Why so? Mostly due to practical bottlenecks, most importantly high computational cost. The computers of the 1990s and early 2000s simply could not handle the parallel computation required to run many experts simultaneously. Typical experiments at that time involved small models even by the standards of the time, often with just a few thousand parameters in total, which did not let researchers exploit the scalability that is the main draw of MoEs.

Besides, there were alternative methods readily available and actually working better. For instance, even the relatively narrow field of ensemble methods specifically were dominated by boosting approaches, starting from AdaBoost and later extended into gradient boosting methods. Boosting is indeed a better way to combine weak submodels, while MoEs begin to shine only as the component models become smarter.

Nevertheless, some research continued. I want to highlight the Bayesian analysis of MoEs and hierarchical MoEs that was developed at the turn of the century (Jacobs et al., 1997; Bishop, Svenskn, 2002). By adding prior distributions to model parameters, Bayesian approaches helped address overfitting on smaller datasets and provided principled uncertainty estimates. These capabilities would prove valuable later when MoEs eventually scaled up, but for now, this theoretical groundwork laid dormant, waiting for the computational resources to catch up.

There were also some practical applications in speech recognition (to model pronunciation variations) and computer vision (for fine-grained classification), but it was done at modest scale and without too much success. With the exception of the above-mentioned Bayesian analysis, MoEs remained largely absent from premier ML conferences.

MoE Renaissance with Outrageously Large Networks

Everything changed dramatically with the 2017 paper called “Outrageously Large Neural Networks” by Google Brain researchers Noam Shazeer et al. (again led by Geoffrey Hinton!). They revitalized mixtures of experts by creatively leveraging GPUs and introducing critical innovations.

The most important was the sparse gating mechanism: rather than activating every expert, they proposed to activate just the top-k experts (typically k=2) per input token, dramatically reducing computational overhead:

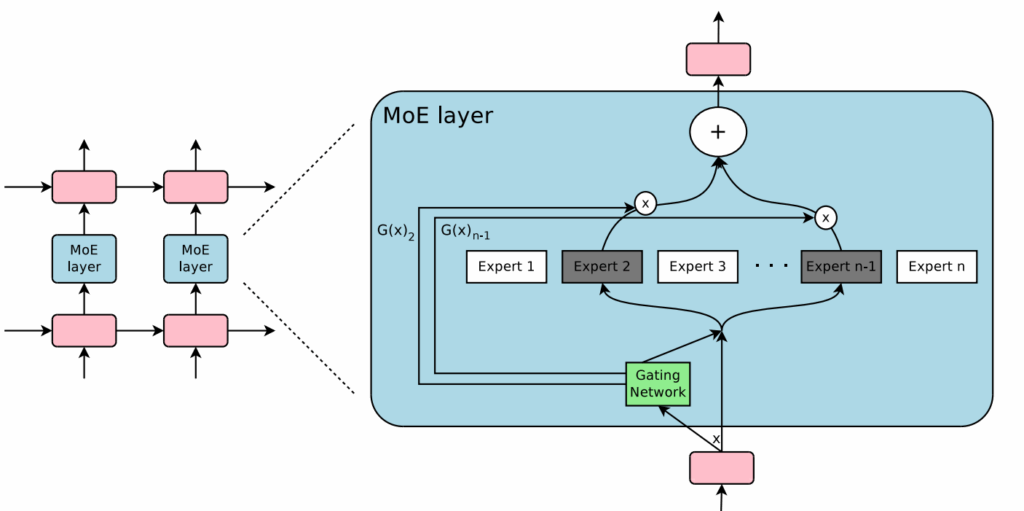
Second, load-balancing auxiliary loss: to avoid the well-known “dead expert” problem (experts receiving zero or negligible input), they introduced a simple but effective auxiliary loss penalizing imbalanced usage across experts. Specifically, they introduced a smoothed version of the load function (probability that a given expert is activated under some random noise distribution) and a loss function that aims to reduce the coefficient of variation in the load.

These improvements enabled Shazeer et al. to build a 137-billion-parameter MoE LSTM (in 2017, that was a huge, huge network!) that matched a dense LSTM with only 1 billion parameters in training costs, a spectacular scalability breakthrough. This work demonstrated how MoEs with conditional computation could efficiently scale to enormous sizes, and revitalized mixtures of experts for the ML community.

The work by Shazeer et al. (2017) laid a foundation that modern MoE models have since built upon, inspiring large-scale implementations that we will discuss below. The underlying concepts—gating networks, localized specialization, and soft probabilistic routing—trace directly back to Jacobs and Jordan’s original formulations, but only with the computational power and practical innovations of recent years MoEs have been elevated from academic obscurity to practical prominence.

Overall, in this section we have retraced the intellectual arc that led from committee machines in the late 1980s to modern trillion-parameter sparsely-gated transformers. Interestingly, many contemporary issues such as dead experts, router instability, and bandwidth bottlenecks were already foreseen in the early literature. If you read Jacobs and Jordan’s seminal papers and related early works carefully, you can still find valuable theoretical and practical insights even into today’s open problems.

After this historical review, in the next sections we will go deeper into contemporary developments, starting with the remarkable journey of scaling language models with sparse conditional computation. Shazeer et al. used LSTM-based experts—but we live in the era of Transformers since 2017; how do they combine with conditional computation?

Scaling Text Models with Sparse Conditional Compute

If the historical journey of mixtures of experts (MoE) was a story of visionary ideas that could not be implemented on contemporary hardware, the next chapter in their story unfolded rapidly, almost explosively, once GPUs and TPUs arrived on the scene. By the early 2020s, scaling language models became the dominant focus of AI research. Yet, the push for ever-larger models soon faced both physical and economic limitations. Mixtures of experts, with their elegant promise of sparsity, offered a way around these limitations, and thus MoEs experienced a remarkable renaissance.

GShard and Switch Transformer

The era of modern MoE architectures began in earnest with Google’s GShard project in 2020 (Lepikhin et al., 2020). Faced with the huge Transformer-based models that already defined machine translation at that time, Google researchers looked for ways to train ultra-large Transformers without the typical explosive growth in computational costs. GShard’s key innovation was to combine MoE sparsity with Google’s powerful XLA compiler, which efficiently shards model parameters across multiple TPU devices.

We are used to the idea that self-attention is the computational bottleneck of Transformers due to its quadratic complexity. However, for the machine translation problem Lepikhin et al. were solving, where the inputs are relatively short but latent dimensions are large, the complexity of a Transformer was entirely dominated by feedforward layers! For their specific parameters (, , input tokens), a self-attention layer took 

   

while a feedforward layer was ~32 times heavier with about

   

In terms of parameter count too, feedforward layers took about two thirds of a Transformer’s parameters (Geva et al., 2020). To put this in perspective: the self-attention computation was like calculating distances between 128 items, while the feedforward layer was like applying 8192 different transformations to each item—a much heavier operation.

So the approach of Lepikhin et al. (2020) was concentrated on feedforward layers. Instead of each Transformer block performing a single dense computation, they replaced half of the dense feed-forward layers with sparsely gated mixture of experts layers (the illustration shows that only every other FF layer is turned into a MoE layer):

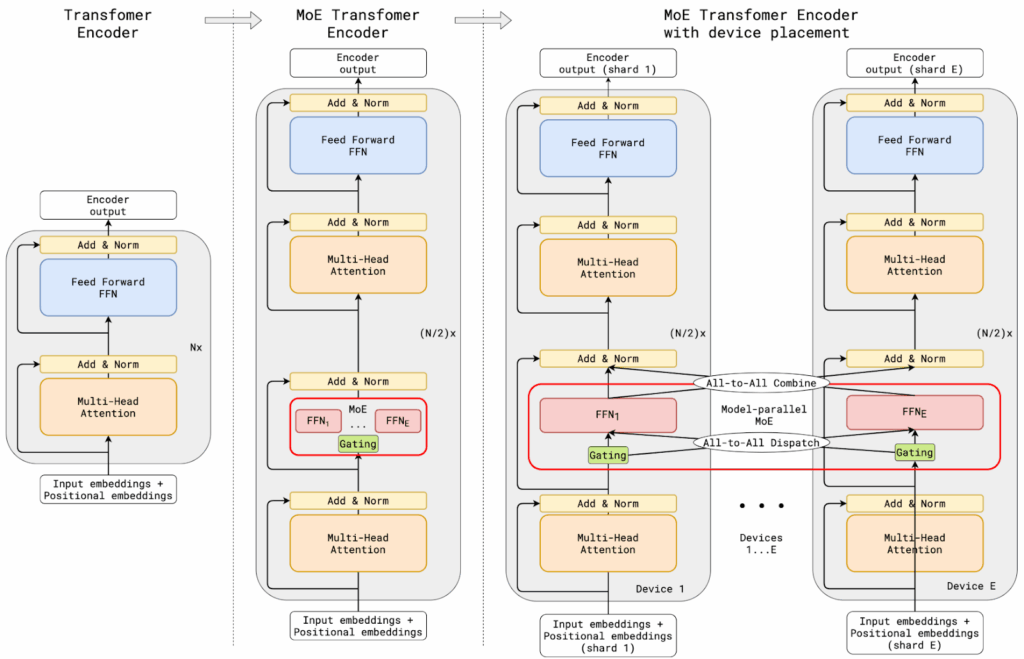
The gating mechanism selectively activates only a handful of experts per input token, thus dramatically reducing the computational load. Gating also included load balancing, this time for training: each expert was assigned a “capacity” value, and on every mini-batch, the number of tokens assigned to an expert cannot exceed this capacity. Lepikhin et al. (2020) also introduced a highly parallel implementation for a cluster of TPUs, which was also very helpful, although perhaps too technical to discuss here.

This allowed GShard to reach previously unattainable scales; ultimately, they trained a 600-billion-parameter machine translation model on 2,048 TPUs over just four days. Moreover, this model delivered a substantial improvement in machine translation metrics compared to dense baselines at similar computational cost.

Another Google Brain project, this time by Fedus et al. (2021), introduced the Switch Transformer in early 2021. Building directly on GShard’s sparse routing idea, the Switch Transformer took sparsity to a more extreme form, implementing a “top-1 routing” mechanism. In GShard, two experts handled each token (unless their capacity was exceeded or one of them had a low weight), but Switch Transformer simplified matters further by activating only the single most appropriate expert per token. Again, this idea was applied to feedforward layers:

This simplification ran contrary to contemporary sensibilities: Shazeer et al. (2017) hypothesized that you have to compare several (at least two) experts to have nontrivial signal for the routing function, and other works studied the number of experts required and found that more experts were helpful, especially in lower layers of the network (Ramachandran, Le, 2018).

Still, Fedus et al. (2021) proved to be right: switching worked just as well as regular gating, only faster. The Switch Transformer was the first to successfully train a model with a trillion parameters! Even more importantly, increasing the number of parameters in this sparse setting still conformed to the famous scaling laws of Kaplan et al. (2020) and allowed training to be much more sample-efficient, i.e., achieve the same results with less data and training compute:

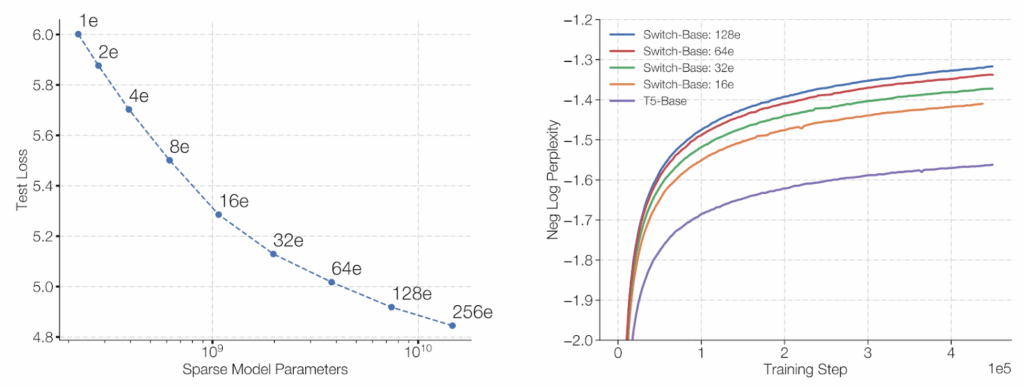
The Switch Transformer emphatically proved that MoE models could not only scale but also remain stable, trainable, and economical. But machine translation was just the beginning.

GLaM and the Pathways approach

Inspired by the groundbreaking successes of GShard and Switch Transformer, later in 2021 Google Research introduced the Generalist Language Model (GLaM; Du et al., 2022), a further improved MoE-based sparse architecture. 

Similar to GShard, GLaM replaces every other Transformer layer with a MoE layer, and at most two experts are activated for every input. But they added recent modifications that the original Transformer architecture had received by that time—Gated Linear Units in feedforward layers (Shazeer, 2020) and GELU activations (Hendrycks, Gimpel, 2016)—and utilized even more aggressive sparsity, activating only 8% of its 1.2 trillion parameters per token. This resulted in GLaM outperforming GPT-3 in both results and computational costs, and in a scaling law that held at least up to 64 experts:

Despite this extreme sparsity, GLaM performed very well on benchmark tasks, often matching or surpassing dense models such as GPT-3 (175B parameters), while using only a fraction (about one-third) of the energy during training.

GLaM was not just a single model with a novel technical breakthrough; it represented a philosophical shift. Google’s broader “Pathways” initiative introduced soon after (Dean, 2021) contained a vision of single models capable of handling multiple tasks and modalities efficiently by selectively activating different parts of the network—pathways—based on context:

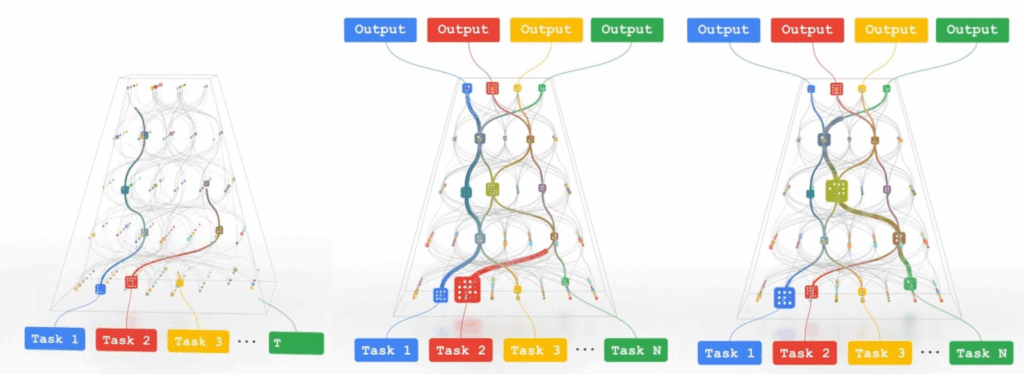
The vision already suggested hierarchical routing strategies, where one router would select broad modality-specific pathways and another would pick fine-grained token-level experts, just like modern multimodal architectures such as Gemini 1.5 do.

The first widely adopted result of this initiative was the Pathways Language Model (PaLM)  LLM released by Google in April 2022 (Chowdhery et al., 2022). While PaLM itself was not a MoE model, it represented Google’s commitment to the broader Pathways vision of conditional computation and served as an important stepping stone towards their later MoE implementations in Gemini. Where GLaM/MoE models saved compute by explicitly sparse activations, PaLM showed that a dense Transformer could still scale to half-a-trillion params if the communication stack is re-engineered. Specifically, PaLM used a client-server graph and gradient exchange between denser compute clusters to achieve near-linear throughput, scaling for the first time to two TPU pods… which let PaLM understand jokes about pods much better:

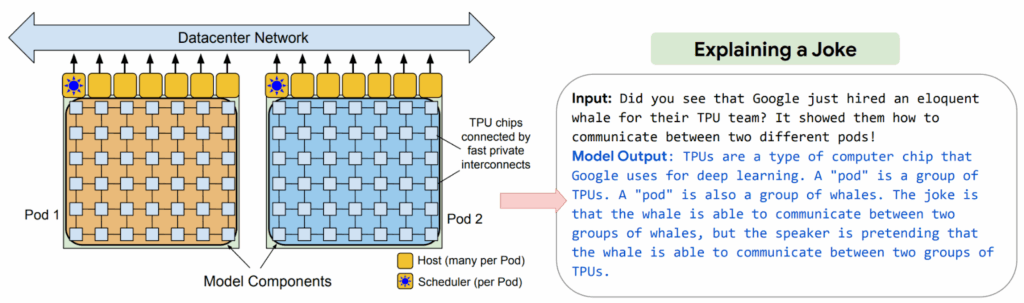
PaLM also popularized chain-of-thought prompting, showing how asking the model to generate its reasoning consistently boosts results across multiple applications. It became a popular and important family of LLMs, leading to PaLM 2 (Anil et al., 2023) and specialized offshoots such as Med-PaLM for medical applications (Singhal et al., 2023a; 2023b) and PaLM-E for embodied reasoning (Driess et al., 2023).

Note that PaLM is not a mixture-of-experts model per se, it is a dense model where every layer is activated on every input. To be honest, it’s not really a full implementation of the Pathways idea either; it runs on the Pathways orchestration level but does not employ the original detailed routing idea. As Chowdhery et al. (2022) put it themselves, “PaLM is only the first step in our vision towards establishing Pathways as the future of ML scaling at Google and beyond”.

Still, it was a great first step and an important stepping stone towards distributed LLM architectures. But when and how did actual MoE models enter the frontier LLM landscape? While PaLM demonstrated the power of dense models with novel distributed orchestration, the fundamental efficiency gains of sparse architectures were still underexplored. Let us see how two major industry players took up the challenge of making MoE models practical and ready for widespread adoption.

DeepSpeed-MoE and Megatron-Core: opensourcing MoE for the masses

In 2022, the landscape of LLMs was not yet as firmly established as today, where new entries such as Grok require huge investments from the richest guys in the world and still kind of fall short. The DeepSpeed family and its Megatron offshoots could try to come anew and define the LLM frontier.

Although, to be fair, there were not one, but two extremely rich companies involved: DeepSpeed was developed by Microsoft researchers, while the Megatron family was trained with the vast computational resources of NVIDIA. They first came together to produce the Megatron-Turing Natural Language Generation model (MT-NLG), which had a record-breaking 530B parameters back in October 2021 and broke a lot of records in natural language understanding and generation tasks (Smith et al., 2022; Kharya, Alvi, 2021).

By mid-2022, both teams of researchers tried to build on this success with sparse architectures. DeepSpeed-MoE (Rajbhandari et al., 2022) set the goal to make mixture of experts models practical for GPT-style language modelling, i.e., cheap to train and, crucially, cheap to serve in production. The paper presents an end-to-end stack that includes new architecture tweaks, compression ideas, distributed training, and an inference engine.

They use top-1 gating (already standard when you want to be fast and cheap), still sparsify only the feedforward parts of the Transformer architecture, and shard each expert into its own GPU rank, mixing data and tensors so that every GPU processes exactly one expert. 

The MoE architectural novelty in DeepSpeed-Moe was the Pyramid-Residual MoE (PR-MoE). The pyramid part means that early layers keep fewer experts, and later layers double them, which reflects the idea that deeper layers learn task-specific concepts. The residual part means that each token always passes through a small dense MLP branch, while the expert acts as a residual “error-corrector”:

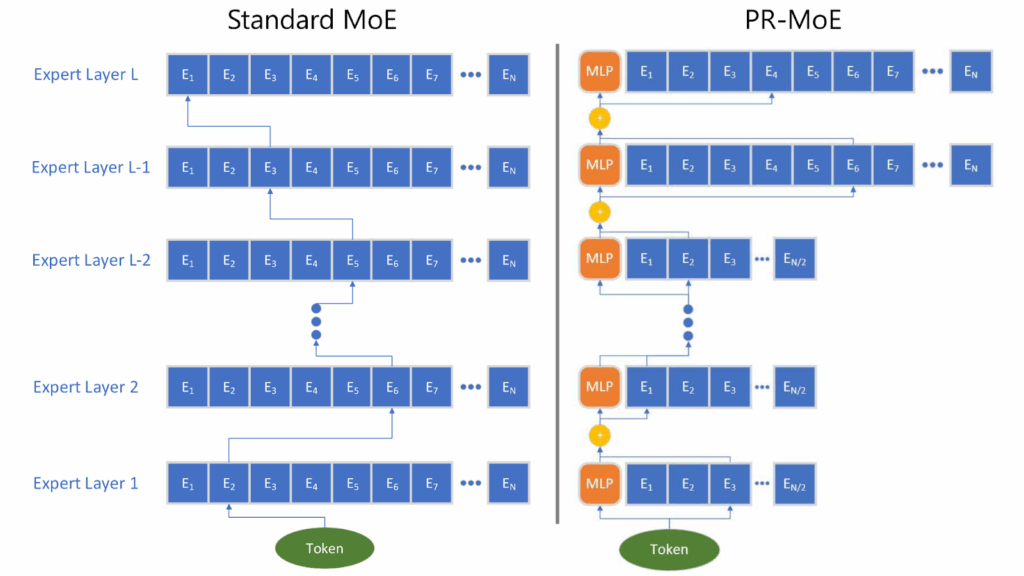
This allowed DeepSpeed-MoE to have up to 3x fewer parameters with virtually identical zero-shot accuracy.

Another interesting trick was about the distillation process that could train smaller MoE ensembles that approach the quality of the original much larger variant. Rajbhandari et al. (2022) noticed that while distillation is a natural idea for MoE models as well (although it was still novel at the time—Artexte et al., 2021 and Fedus et al., 2022 distilled MoE models before, but only into dense smaller Transformers), it starts to hurt the results after a while if you just distill larger experts into smaller ones. Thus, they introduced Mixture-of-Students (MoS) distillation: the student experts copy the teacher for the first 40% of pretraining, and then distillation is turned off so the students can keep minimizing their own LM loss.

All of these innovations—and many more—have made their way into an open source release. The DeepSpeed library, still supported and improved by Microsoft researchers, emerged as a very influential open source framework. For MoE models specifically, it offers CUDA kernels optimized for sparsity together with sophisticated memory management techniques, and later developed DeepSpeed’s ZeRO-3 memory partitioning method (from Zero Redundancy Optimizer, first introduced by Rajbhandari et al., 2019; see also ZeRO++ by Wang et al., 2023) further pushed scalability, allowing massive MoE models to run on relatively modest hardware configurations.

NVIDIA’s Megatron-LM suite, which includes the Megatron-Core framework with MoE implementations, followed shortly thereafter, introducing specialized kernels known as Grouped-GEMM, which efficiently batch many small expert computations into a single GPU operation. Megatron-Core also pioneered capacity-aware token dropping and systematic monitoring tools to alleviate common MoE issues like dead experts. These innovations significantly streamlined training pipelines, accelerating adoption of MoE at scale across diverse applications. What’s more, the Megatron-LM suite is also published in open source and has become the basis for many interesting research advances (Shoeybi et al., 2019; Shin et al., 2020; Boyd et al., 2020; Wang et al., 2023; Waleffe et al., 2024).

While DeepSpeed and Megatron showed that it was feasible to scale MoEs up, the real test would come with their adoption in production systems serving millions of users. In the next section, we will examine how today’s frontier LLMs have embraced and extended these ideas. Are state of the art LLMs powered by MoEs or have they found a better way to scale?

Mixtures of Experts in Flagship LLMs

Actually, the answer is yes. Between 2023 and 2025, MoE architectures firmly transitioned from research artifacts to production-ready frontier models. Let me show three prominent models that exemplify this shift.

Mixtral of Experts

It is fashionable to frown upon Mistral AI, a European research lab whose top models indeed often do not match the best American and Chinese offerings in scale and capabilities, and the EU AI Act and other associated bureaucracy is not helping matters.

But they are committed to open source, where they make significant contributions to the field, and the Mixtral family rapidly became an open-source sensation in 2023. Specifically, we are interested in the Mixtral of Experts idea (Jiang et al., 2024; Mistral AI, 2023) and its 8x7B model based on the Mistral-7B backbone (Jiang et al., 2023) that has entered plenty of baseline comparisons and has given rise to a lot of research papers. 

Mixtral 8x7B is relatively small: 47B total parameters with 13B of them active per token, 32 layers with 8 experts per layer and top-2 routing, and only 32K tokens of context. The MoE implementation is straightforward—when a token arrives at a feedforward layer (again, here we leave the self-attention layers unchanged), a router scores it into 8 logits, only the top 2 survive, and their outputs are combined in a linear combination:

Unlike previous MoE architectures, Mixtral 8x7B has small fan-out (only 8 experts) but top-2 routing instead of the common top-1 choice; this seems to provide a better quality-compute trade-off, and 13B active parameters fit on commodity GPUs, so many researchers could run Mixtral 8x7B for their projects without huge funding.

The Mistral AI team also studied which experts get activated for which tokens. 

And here is an illustration of which experts get activated on which tokens for several layers in the architecture (Jiang et al., 2024); note that it’s less semantic and perhaps more syntactic than you would expect, especially at top layers:

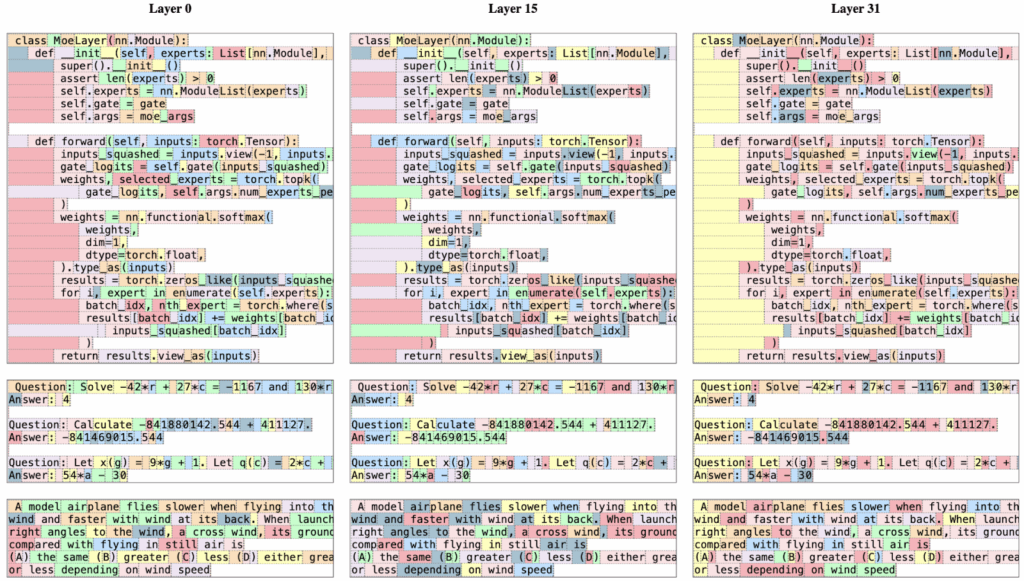
With good clean multilingual training data, Mixtral 8x7B became the first open-source MoE that rivaled GPT-3.5 on average while running on a single GPU.

Gemini 1.5 Pro

Google’s flagship model, Gemini 1.5 (Gemini Team, 2024), showcased multimodal routing across text, images, audio, and video, delivering previously unimaginable context windows—up to an astonishing 10 million tokens.

Again, Gemini 1.5 Pro replaces most of the dense feed-forward blocks with MoE blocks, routing every token to a small subset of experts. The main difference from previous MoE iterations was that previously MoE LLMs were unimodal, topped out at 2–32K tokens of context, and their expert routing was still fairly simple. Gemini 1.5 introduces a multimodal encoder-decoder, raises the context size up to millions of tokens, and introduces a more careful gating scheme (materials mention DSelect-k by Hazimeh et al., 2021, which we will discuss below), so load balancing stays healthy even when the prompt is a 700K-token codebase.

Gemini also introduced intricate caching strategies, such as cross-expert KV-cache sharing, which led to significant gains in cost efficiency and, again, context enlargement.

GPT-4 and later OpenAI models

OpenAI is notoriously not that open with its research ideas (and perhaps they are quite correct in that!), so I cannot really tell you what were the novelties of GPT-4o in detail; all we have officially are the system cards for GPT-4 (OpenAI, 2023) and GPT-4o (OpenAI, 2024), which are both mostly about capabilities and safety rather than about the ideas. So the following details should be taken as informed speculation rather than confirmed facts.

But there have been leaks and analyses, and I can link to a Semianalysis post on GPT-4 that suggests that GPT-4o (and its base model GPT-4) employs approximately 16 experts per MoE layer, each with around 111 billion parameters, amounting to roughly 1.8 trillion total parameters with around 280 billion active at any given time; see also here and here.

While the exact number of parameters may be different, it’s almost certain that starting from GPT-4, OpenAI’s latest models are all of the MoE variety. This lets them both be huge and at the same time have reasonable runtimes. GPT-4 routes to the top 2 experts out of 16, and there are, it seems, specialized experts fine-tuned to do specific stuff, e.g., one expert concentrates on safety and another on coding. GPT-4o seems to have the same basic structure but several efficiency improvements that are about, e.g., sparse attention mechanisms rather than MoE.

Note that GPT-4 is still the workhorse of the latest reasoning models such as o4-mini, o3 and o3-pro; the release of a larger model, GPT-4.5 (OpenAI, 2025), was not that successful, and while I cannot be 100% sure it seems like all top OpenAI’s offerings are still GPT-4-powered.

DeepSeek-V3

The Chinese top tier model, DeepSeek-V3 (DeepSeek AI, 2024), which soon became the basis for the famous DeepSeek-R1 reasoning model (Guo et al., 2025), pushes breadth: lots of fine-grained experts, relatively large K, sophisticated router engineering to keep them busy, and a lot of very insightful tricks in the training process to make the giant 671B parameter model as efficient as possible. Here let me refer to my previous longform post where I went into some details about the engineering ingenuity of DeepSeek-V3.

Llama 4

Probably the latest frontier family of models that we do have detailed information about is the Llama 4 family, introduced in April 2025 (Meta AI, 2025). And fortunately for us now, instead of using a dense decoder-only transformer like the Lllama 3 family, Llama 4 became the first of the Llama models to implement a MoE-based architecture.

For example, the Llama 4 Maverick model employs a large MoE architecture with 128 experts per layer and top-2 routing, meaning that each token activates 2 experts out of 128. The total parameter count reaches over 400 billion, but only about 17B parameters are active per token, making it efficient to run. One of these two experts in the Llama 4 family is a shared expert:

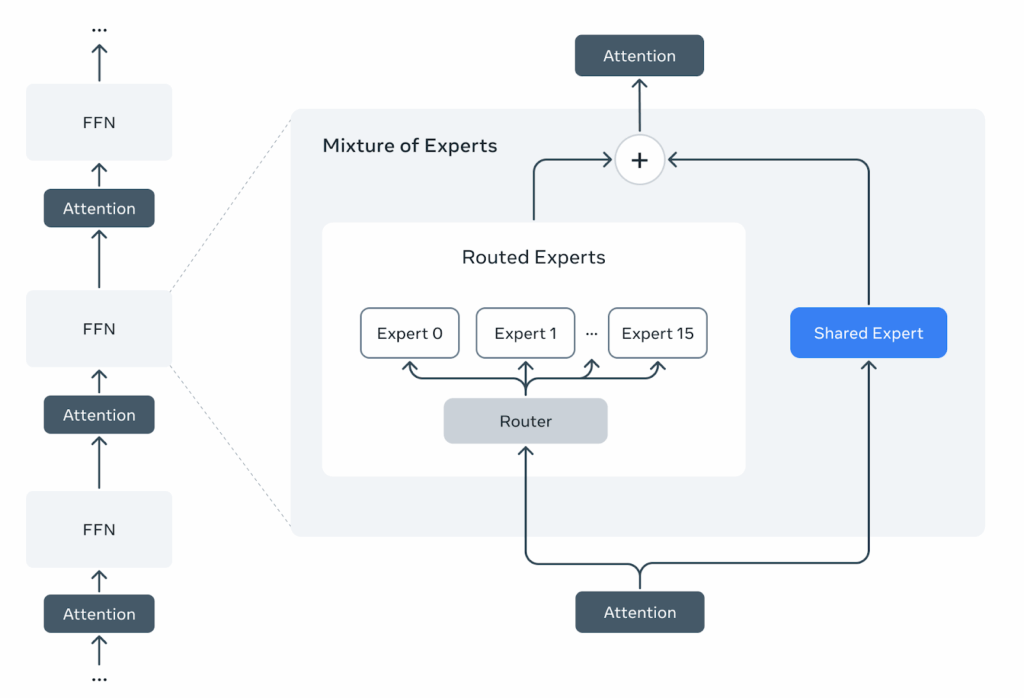
The model also introduced several innovations in the Transformer architecture itself, in particular the iRoPE approach with interleaved attention layers without positional embeddings. Perhaps most importantly for the open-source community, Meta released not just the model weights (on Huggingface) but also detailed training recipes and infrastructure code (on GitHub), making it a great starting point for others to train their own MoE models at scale.

With that, we are already basically at the frontier of modern LLMs; latest improvements deal with fine-tuning strategies and turning one-shot LLMs into reasoning models, which do not change the underlying model structure. So let me end the high-level survey part of the post here and proceed to actually diving into the details of routing strategies and other architectural choices that a MoE model designer has to make.

Router Mechanics: How To Train Your Monster

Mixtures of experts sound very simple from a bird’s eye view: you have lots of small, specialized networks (“experts”), and for every input, you activate just a few, as chosen by a router which is also a subnetwork. But translating this elegant idea into reality involves many important practical considerations. How exactly do routers work? What other considerations are there? In this section, let’s dive beneath the surface and explore exactly how engineers tame this beast in practice.

Sparse vs. dense MoEs

The first important distinction is between dense and sparse MoEs: do we combine the experts in a full linear combination or do we choose a small subset of the expert? Here is an illustration by Cai et al. (2024):

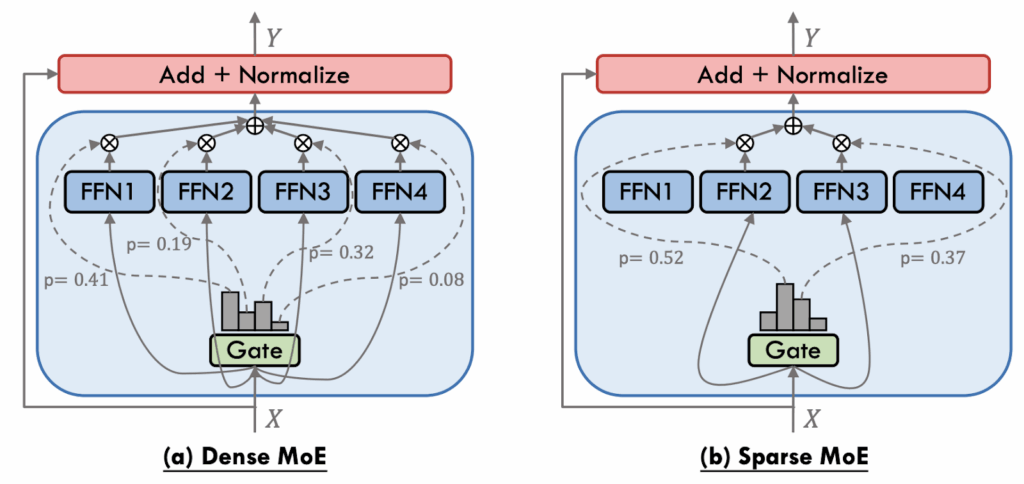
Formally speaking, a dense MoE router produces some vector of scores , where are the router’s parameters and is the input, and then uses it as softmax scores:

   

where are the weights of the experts. A sparse MoE router only leaves the top of these scores and sets the rest to negative infinity so that the softmax would lead to zero probabilities:

   

Early works mostly used dense MoEs (Jordan, Jacobs, 1991; 1993; Collobert et al., 2001). But ever since GShard that we discussed above (Shazeer et al., 2017) had introduced and popularized sparse routing, it was the common agreement that sparse routing is the way to go as a much more efficient solution: you don’t have to activate all experts every time. 

The only remnants of dense MoEs were shared experts, pioneered by the DeepSpeed-MoE (Rajbhandari et al., 2022) architecture that we discussed above. In this case, every token is processed by a fixed expert (which is “densely activated”, so to speak) and another expert chosen through gating, so it is actually top-1 gating with two resulting experts.

It has been known that dense MoEs might work better—see, e.g., Riquelme et al. (2021)—but the tradeoff has been generally assumed to be not worth it. Still, interestingly, work on dense mixtures of experts has not stopped, and sometimes it has been very fruitful. Let me highlight a few of these cases; they are very different but each explores alternatives to the classical sparsely-gated Top-k MoE layer.

EvoMoE (Evolutional Mixture-of-Experts; Nie et al., 2021) introduces two-phase training. On the expert-diversify phase, they start with one shared expert, then copy and randomly mask it to spawn many diverse experts. On the gate-sparsify phase, they introduce the Dense-to-Sparse (DTS) gate: a softmax that initially routes tokens to all experts but then gradually prunes itself until it behaves like a sparse Top-1 or Top-2 routing gate. Here is an illustration by Nie et al. (2021):

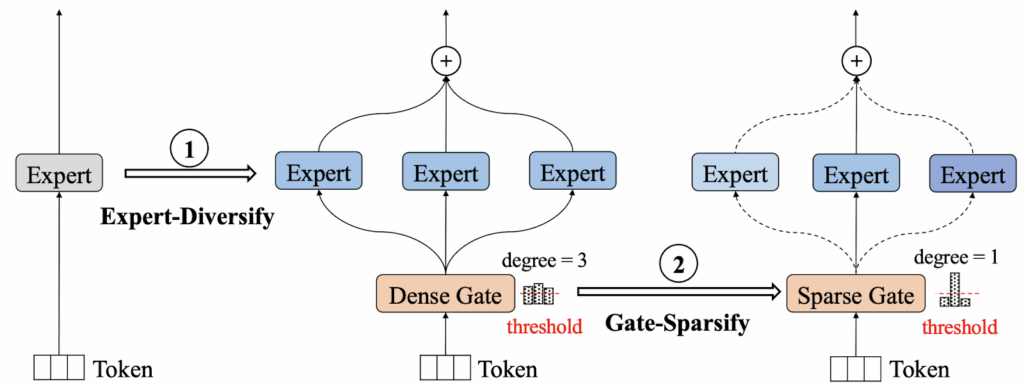
As a result, routing is fully dense at the beginning, allowing every expert to receive gradient signals; sparsity is imposed only after experts have specialized, so in this case the authors try to get the best of both worlds with a hybrid training procedure.

MoLE (Mixture of LoRA Experts; Wu et al., 2024) notices that sparseness is important when experts are large, but there are use cases when they aren’t. What if your experts are LoRA adapters? Then you can treat every independently trained LoRA as an expert and learn a hierarchical soft-max gate that mixes them layer-by-layer.

The idea is to get an economical but expressive way to learn to adaptively combine different LoRAs; here is a comparison vs. linear composition (left) and reference tuning (center), two other popular methods for LoRA composition:

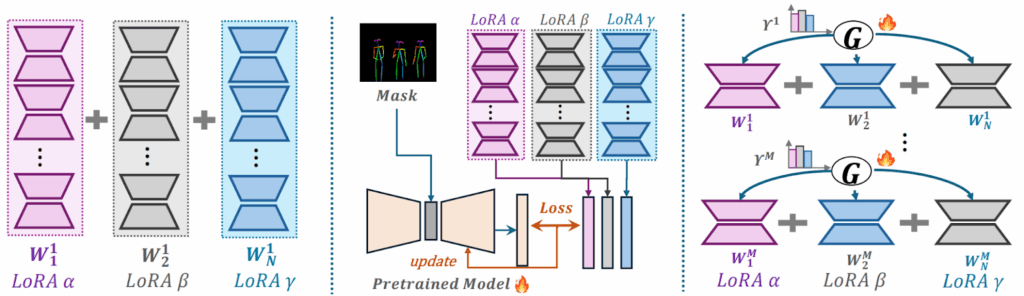
Moreover, because the routing gate is continuous, MoLE can later mask unwanted experts at inference time and renormalize weights without retraining. Wu et al. (2024) introduce a gating balance loss that keeps experts alive and avoids dominance by a few adapters. As a result, they get an approach that can scale to dozens of adapters with little extra memory because only the tiny routing gate is trainable.

Another creative way to combine LoRA adapters with a MoE mechanism was introduced in LoRAMoE (Dou et al., 2024). Compared to standard MoE, LoRAMoE replaces each feedforward layer by a mini-MoE whose experts are low-rank LoRA matrices; the output is a dense weighted sum over all experts:

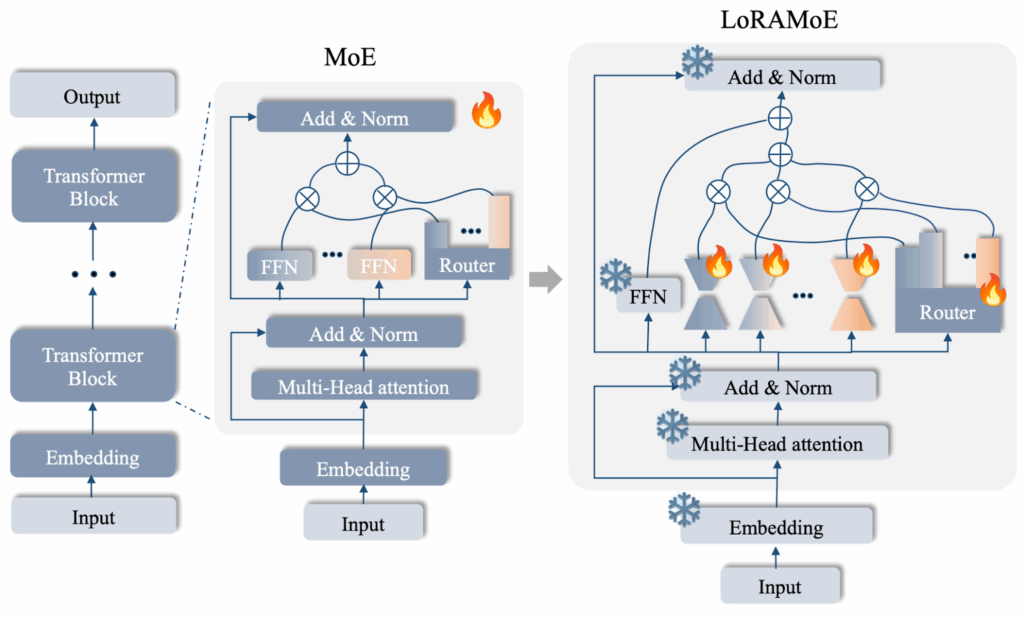
Basically, just freeze the backbone, plug in multiple LoRA adapters as experts and blend them with a dense router. Moreover, Dou et al., (2024) specialize their experts explicitly, introducing a localized balancing constraint that biases half of the experts towards knowledge-heavy tasks and half towards instruction following (we are talking about image-to-text models here).

Interestingly, they applied it to LLMs and found that dense MoE and a frozen backbone preserve pretrained world knowledge much better than full SFT or single-LoRA tuning. After fine-tuning on specific downstream tasks, the LoRAMoE architecture lost much less performance on general question answering benchmarks about the world than the alternatives.

As you can see, sparse vs. dense MoE is not a dichotomy but more of a spectrum: you can switch between pure dense and pure sparse MoE in training, or apply dense MoEs to smaller subnetworks, or use any other hybrid approach that might be preferable in your specific case.

MoPE and where to place it

The discussion of MoLE and LoRAMoE brings us to a whole different class of MoE-based architectures: Mixtures of Parameter-Efficient Experts (MoPE). MoPE is a design paradigm that combines two ideas that had previously advanced largely in parallel:

• the conditional computation and specialization benefits of MoEs and
• the memory- and compute-friendly techniques of parameter-efficient fine-tuning (PEFT) such as LoRA, conditional adapters, prefix tuning and others (see, e.g., a detailed survey by Han et al., 2024).

In MoPE, the heavy dense backbone of a pretrained LLM is frozen, and each expert represents a lightweight PEFT module. A gating network selects, per token or per example, the subset of PEFT experts that will be applied on top of the frozen weights. The idea is to combine the task-adaptivity and routing diversity of MoEs while not actually spending the storage and FLOPs budget usually associated with sparse expert layers. It was pioneered by MoELoRA (Liu et al., 2023) and MixLoRA (Li et al., 2024) and has blossomed into a subfield of its own.

Since we are talking about PEFT now, there is a wide variety of different places where one can put the adapter inside a standard Transformer stack of the base model. Here I will again use an illustration by Cai et al. (2024) with a general taxonomy of these placements, and then we will consider them one by one:

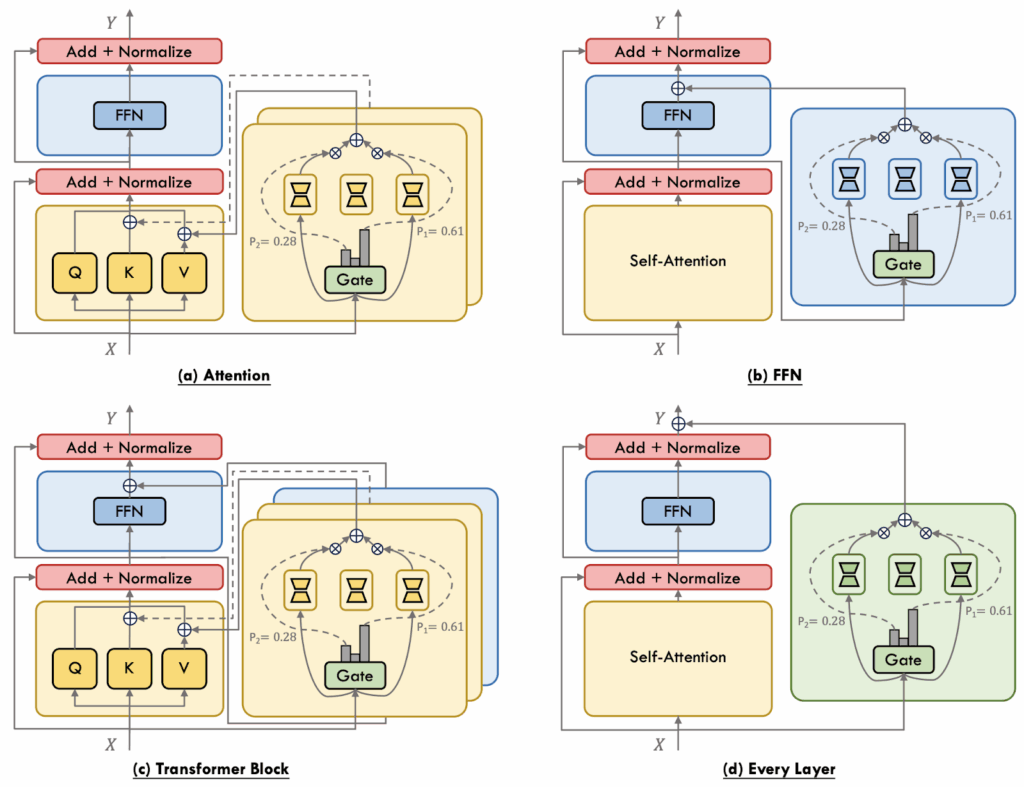
In attention-level MoPE, experts augment individual projection matrices (Q, K, V, O). E.g., MoELoRA (Liu et al., 2023) inserts multiple LoRA experts into the Query and Value projections and uses top-k routing plus a contrastive loss to encourage expert diversity and stable routing. MoCLE (Gou et al., 2024) clusters tasks first and then routes inputs to cluster-specific LoRA experts plus a universal backup expert.

FFN-level MoPE adapts the feedforward sublayer, as classical MoEs usually do, but instead of gating the full FFN parallel PEFT experts are added and combined through gating. AdaMix (Wang et al., 2022) pioneered this setting, using adapter experts with a stochastic routing policy at training time that collapses to a cheap ensemble at inference, while MixDA (Diao et al., 2023) places domain-adapters and task-adapters sequentially to disentangle domain and task knowledge. LoRAMoE (Dou et al., 2024) that we have discussed above also belongs to this class.

In Transformer-block-level MoPE, two expert pools are attached simultaneously—one modulating the self-attention block, the other the FFN. For example, MoV (Zadouri et al., 2024) replaces both blocks’ dense parameters with tunable vectors, showing large memory savings without sacrificing quality, while MoLoRA from the same work follows the dual-pool idea but sticks to LoRA experts. UniPELT (Mao et al., 2024) mixes heterogeneous PEFT methods (adapter, prefix, LoRA) under separate gates, letting the model pick the most suitable adaptation mechanism per input.

Finally, layer-wise (or every-layer) MoPE treats the entire Transformer layer as the unit of specialization, with each layer hosting a set of PEFT experts applied to the whole block.  We have discussed MoLE (Wu et al., 2024) that views already-trained LoRAs as ingredients and learns only the gating weights to compose them on-the-fly for a new domain. Omni-SMoLA (Wu et al., 2024) extends the idea to three modality-specific expert sets (text, vision, and multimodal) for vision-and-language tasks.

Training regimes

Another design choice that a MoE system has to make is how exactly to train the experts. Early MoE systems such as GShard and Switch Transformer simply replaced each feed-forward block with a sparse MoE layer and trained the entire network end-to-end; inference mirrored the training configuration without architectural changes. This approach remains a standard baseline, but by now there are three major routes that one can follow to try and improve upon it.

Dense-to-sparse regime starts with a dense backbone and gradually introduces sparsity.  For example, Residual MoE (RMoE; Wu et al., 2022) pretrains a Vision Transformer densely, then fine-tunes it with sparsely activated experts while aligning outputs between the original FFN and the emerging MoE layer. EvoMoE (Nie et al., 2021) that we have discussed above bootstraps knowledge with a single expert, then spawns additional experts, and employs a Dense-to-Sparse Gate (DTS-Gate) that performs gradual annealing from full activation to top-k routing, thus alleviating the cold start problems for experts. The Sparse Upcycling approach (Komatsuzaki et al., 2023) copies FFN weights from a well-trained dense checkpoint into multiple identical experts, adds a randomly initialized router, and then retrains the network. DS-MoE (Pan et al, 2024) and SMoE-Dropout (Chen et al., 2023) are hybrid approaches that alternate between dense and sparse activations during training so that all experts receive gradient signal (this is needed to avoid expert under-utilization), but inference reverts to sparse execution for efficiency.

Sparse-to-dense distillation or pruning aims for deployability: how do we compress a high-capacity sparse MoE into a latency-friendly dense model. For example, Switch Transformer (Fedus et al., 2021) distills knowledge into a dense student with only ~5% of the parameters, while OneS (Xue et al., 2023) first aggregates expert weights by SVD or top-k heuristics, then distills into a single dense model that can keep 60–90 % of the parent’s gains across vision and NLP tasks. ModuleFormer (Shen et al., 2023) and Expert-Slimming / Expert-Trimming strategies by He et al. (2024) prune under-used experts or average their weights back into a single FFN, yielding a structurally dense network that preserves most task accuracy while significantly reducing memory and communication costs. In general the Sparse-to-Dense training mode demonstrates that MoE can serve as a training scaffold: once knowledge has diversified across experts, it can be re-fused into a compact model without full retraining.

Finally, expert-model merging means that experts are trained independently and then fused together with a router. For example, the Branch-Train-Merge (BTM; Li et al., 2022) and Branch-Train-MiX (BTX; Sukhbaatar et al., 2024) pipelines train several dense experts independently on domain-specific data and later fuse their FFNs into a single MoE layer, leaving attention weights averaged. Then MoE is briefly fine-tuned in order to teach the router to exploit this cross-domain complementarity. The Fusion of Experts (FoE; Wang et al., 2024) framework generalizes this idea, treating merging as supervised learning over heterogeneous expert outputs. Expert-model merging avoids the heavy communication of joint MoE training and allows recycling of preexisting specialist checkpoints, which is particularly attractive when there are external reasons against combined training such as, e.g., privacy concerns.

Obviously, the dimensions of sparse vs. dense routing, PEFT placement, and training modes are orthogonal, and there have been plenty of different variations for each of these ideas; let me again link to the surveys here (Cai et al., 2024; Masoudnia, Ebrahimpour, 2024; Mu, Lin, 2025). Moreover, these are not even the only dimensions. One could also consider different ways to feed training data or different engineering approaches to sharding the experts on a computational cluster and organizing communication between them. But I hope that this section has given you a good taste of the diversity of MoE approaches, and perhaps we will investigate some other dimensions in the second part.

Conclusion

The journey of mixtures of experts has been a journey from relatively obscure ensemble methods that couldn’t quite find a good problem fit to the backbone of frontier AI systems. This evolution offers several important lessons about innovation in machine learning and points toward some future directions.

First, timing matters as much as brilliance. The core MoE ideas from Jacobs et al. (1991) were essentially correct—they just arrived twenty-five years too early. Without GPUs, distributed computing, and modern optimization techniques, even the most elegant algorithms remained academic curiosities. This pattern repeats throughout ML history. For example, the main ideas of Transformer architectures were arguably already introduced in the attention mechanisms of the early 1990s but needed computational scale to shine, diffusion models had spent years in relative obscurity before efficient sampling algorithms were developed, and reinforcement learning required massive simulation infrastructure to tackle large-scale problems. The lesson for researchers is both humbling and hopeful: your “failed” idea might just be waiting for its technological moment, and also, perhaps, we will hear more about other “failed” ideas in the future, when the time is right.

Second, sparsity is not just an optimization trick—it is an important design principle. The success of MoE models demonstrates that by activating only 1-10% of parameters per input, we can achieve what dense models cannot: gracefully scale to trillions of parameters while maintaining reasonable inference costs. This sparse activation pattern mirrors biological neural networks, where specialized regions handle specific functions, and human organizations, where human experts collaborate dynamically based on a specific task. Perhaps the future of AI lies not in ever-larger monolithic models but in large ecosystems of specialized components, assembled on-demand for each specific problem.

Third, the best architectures balance elegance with engineering. Every successful MoE implementation requires both theoretical insights and pragmatic engineering; we have talked about the former in this first part, and next time we will talk some more about the latter.

In the second part of this mini-series, we will explore how these same MoE principles are transforming computer vision and multimodal AI, where the routing problem becomes even more fascinating: how do you decide which experts should handle a pixel, a word, or the boundary between them? The principles we have explored—sparse activation, specialized expertise, dynamic routing—take on new dimensions when applied across modalities. Stay tuned!

Sergey Nikolenko
Head of AI, Synthesis AI